Aralık

Aralık: iki sayı arasındaki tüm sayılar demektir.

Örneğin: 1 ve 6 arasındaki tüm sayılar bir aralık belirtir

Tüm Sayılar Mı?

Evet. Bu iki değer arasında yer alan tüm gerçek sayılar bu aralığa girer.

Örneğin: 2 ile 4 arasında şunlar vardır:

2.1

2.1111

2.5

2.75

2.80001

⁷/₂

3.7937

Ve daha fazlası!

Peki Aralıkta Belirtilen Sayılar Dahil Mi?

Hmmm... Bazen dahildir, bazen de değildir. Bunu belirtmemiz gerekir.

Örneğin: "20 kg'a kadar paketler kabul edilir"

Eğer paketiniz tam 20 kilo ise ... dahil mi yoksa dahil değil mi?

Bu açıkça belirtilmemiş.

Bunu kesinleştirirken üç şekilde ifade edebiliriz:

Eşitsizlik
Sayı doğrusu
Aralık işareti

Eşitsizlikler

Eşitsizliklerde şunları kullanırız:

> büyüktür
≥ büyük ve eşittir
< küçüktür
≤ küçük ve eşittir

Bunun gibi:

Örneğin: x ≤ 20

Bize diyor ki: "x, 20'den küçük veya eşittir"

Yani: 20 dahil ve 20'ye kadar olan sayılar

Aralık İşareti

Bir "aralık işareti" başlangıç ve bitiş sayıları ile:

[ ] köşeli parantez, belirttiğimiz sayılar da dahilse kullanılır veya
( ) parantez, dahil değilse kullanılır

Şunun gibi:

Interval Notation

Örneğin: (5, 12]

Şu anlama gelir: Aralığımı 5'ten 12'ye kadardır, 5 dahil değildir ama 12 dahildir

Sayı Doğrusu

Sayıları bir doğruya yazmak
hangisinin büyük ya da küçük olduğunu görmemizi kolaylaştırır.



Negatif Sayılar (-)	Pozitif Sayılar (+)
(Doğru sol ve sağ tarafa doğru sonsuza kadar gider.)

Soldaki bir sayı, sağdaki bir sayıdan daha küçüktür.

Örneğin:

5, 8'den küçüktür
−1, 1'den küçüktür
−8, −5'den küçüktür

Sağdaki bir sayı, soldaki bir sayıdan daha büyüktür.

Examples:

8, 5'ten büyüktür
1, −1'den büyüktür
−5, −8'den büyüktür

Sayı doğrusu üzerinde işaretleme yaparak aralık gösterebiliriz. Bunun için sayılar arasını kalın bir çizgi ile belirtiriz, ve:

sınır belirten değer dahilse içi dolu bir çember çizeriz
dahil değilse içi boş bir çember çizeriz

Şunun gibi:

Örneğin:

(0, 20)

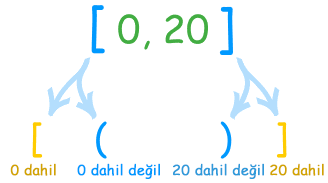
Şu anlama gelir; 0 ile 20 arasındaki sayılar, 0 dahil değil ama 20 dahildir

Üç Yöntem Bir Arada

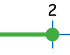
Üç farklı yolu tek tabloda gösterirsek (Aralık 1 ile 2 arasındadır):

	1'den		2'ye
	1 Dahil	1 Dahil Değil	2 Dahil Değil	2 Dahil
Eşitsizlik:	x ≥ 1 "büyüktür ve eşittir"	x > 1 "büyüktür"	x < 2 "küçüktür"	x ≤ 2 "küçüktür ve eşittir"
Sayı doğrusu: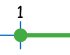
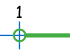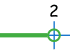Aralık işareti:	[1	(1	2)	2]

Örneğin: 1 dahil olsun ama 2 dahil olmasın:

Eşitsizlik:

x ≥ 1 ve x < 2

veya birlikte: 1 ≤ x < 2

Sayı doğrusu:

Aralık işareti:

[1, 2)

Çeşitli Örnekler

Örnek: "Ne alırsan 10 lira"

Bunun anlamı ne satılıyorsa 10 dahil ve 10 liradan ucuz.

Ve tabiki şunu da söylememiz doğru olur, fiyatlar 0 liradan fazladır.

Bunu eşitsizlik olarak şöyle gösteririz:

Fiyat ≤ 10 ve Fiyat > 0

Bu ikisini birleştirelim:

0 < Fiyat ≤ 10

Sayı doğrusunda şöyle görünecektir:

(0, 10]

Ve aralık işareti ile basitçe:

(0, 10]

Açık Ya Da Kapalı

Bir aralık sınırının "Açık" ya da "Kapalı" olması, son değerin dahil olup olmadığını bize bildirir:

(a, b)	a < x < b	açık aralık
[a, b)	a ≤ x < b	soldaki kapalı, sağdaki açık
(a, b]	a < x ≤ b	soldaki açık, sağdaki kapalı
[a, b]	a ≤ x ≤ b	kapalı aralık

Bu aralıklar sonludur. Ayrıca bazı aralıklar sonsuz da olabilir.

Sonsuzluk

Sonsuzluk genellikle aralık işaretlerinde kullanılır.

Sonsuzluk gerçek bir sayı değildir, buradaki anlamı "devam ediyor ..." dur

Örnek: x 3'e eşittir ya da 3'ten büyüktür:

[3, +∞)

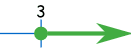
[3, infinity)

Not: Sonsuzluk işaretini kullandıysak aralığımızı yuvarlak parantez ile kapatırız, çünkü ona ulaşamayız!

4 muhtemel "sonsuzluk bitişi" vardır:

Aralık	Eşitsizlik
(a, +∞)	x > a	"a'dan büyüktür"
[a, +∞)	x ≥ a	"a'dan büyük ya da ona eşittir"
(-∞, a)	x < a	"a'dan küçüktür"
(-∞, a]	x ≤ a	"a'dan küçük ya da ona eşittir"

Bu şekilde limitsizliği de gösterebiliriz: (-∞, +∞)

İki Aralık

Bazen iki veya daha fazla aralık belirtmemiz gerekebilir.

Örnek: x ≤ 2 or x >3

Sayı doğrusunda şöyle görünür:

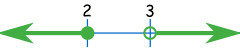
two intervals

Ve aralık işareti kullanarak şu şekilde görünür:

(-∞, 2] U (3, +∞)

Burada kullandığımız "U" birleşim işaretidir.

Not: Yukarıdaki tarz eşitsizliklerde dikkatli olmalısınız.
Tek bir eşitsizlik içerisinde yazmaya çalışmayın:

2 ≥ x > 3 ( wrong)

Çünkü anlam taşımaz (Aynı anda 2'den
küçük ve 3'ten büyük olamaz).

Birleşim ve Kesişim

Az önce iki eşitsizliği "Birleşim" kullanarak birleştirmeyi anlattık (Ve ∪ sembolünü kullandık).

Ayrıca "kesişim" işareti de kullanabiliriz. Örneğin "Nerede kesiştiler?" tarzı bir soru sorabiliriz.

Kesişim sembolünü kullanmalıyız: ∩

Example: (-∞, 6] ∩ (1, ∞)

İlk aralık 6'ya eşit veya küçük olduğunu söylüyor

İkinci aralık 1'den büyük olduğunu söylüyor (Ama 1'e eşit değil)

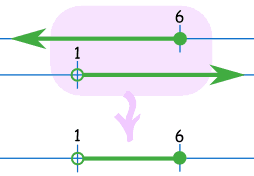
Bu iki kümenin kesişimi 1 - 6 arasıdır (1 dahil değil, 6 dahil):

(1, 6]

Sonuç

Bir aralık iki sayı arasındaki tüm sayıları ifade eder.

Aralığın sınırlarındaki sayıların dahil olup olmadığı önemlidir.

Üç farklı şekilde aralıklar ifade edilebilir: Eşitsizlik, sayı doğrusu ve aralık işareti.