Denklemlerin Çözümü
Bir denklem iki şeyin eşitliğini bildirir. Denklemler eşittir ("=") işareti bulundururlar:
7 + 2 = 10 − 1
Bu denklemin bize söylediği: soldaki işlemin (7 + 2) sonucu ile sağdaki işlemin (10 − 1) sonucu birbirine eşittir
Kısaca "bu buna eşittir" anlamı taşır
Burada başka bir denklem var:
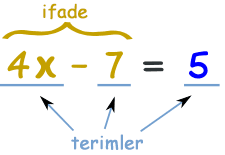
Çözüm Nedir?
Çözüm, bir değişken yerine koyabileceğimiz değer demektir (örneğin x). Öyle bir değer ki denklemi doğrulamalı.
Örneğin: x − 2 = 4
Ne zaman x yerine 6 koyarsak:
6 − 2 = 4
denklem doğru olur
O halde x = 6 bir çözümdür.
Peki x'in başka değerleri de denklemi doğrular mı?
- x = 5 olsaydı "5−2=4" doğru değildir, o halde x=5 bir çözüm değildir.
- x = 9 olsaydı "9−2=4" doğru değildir, o halde x=9 bir çözüm değildir.
- ...
Bu durumda x = 6 tek çözümdür. Buna denklemin kökü deriz.
Daha Fazla Çözüm
Bir denklemi çözen birden fazla çözüm olabilir.
Örneğin: (x−3)(x−2) = 0
x = 3 olursa:
(3−3)(3−2) = 0 × 1 = 0
doğru olur
Eğer x = 2 olursa:
(2−3)(2−2) = (−1) × 0 = 0
yine doğru olur
Bu durumda çözümler:
x = 3 veya x = 2
Tüm çözümleri bir araya topladığımızda Çözüm Kümesini elde ederiz
Çözümler Her Yerde!
Bazı denklemler her durumda doğrudur. Bunlara özdeş denklemler deriz.
Örneğin: Trigonometrik bir özdeşlik:
tan(θ) = sin(θ)/cos(θ)
Denklemi Nasıl Çözeriz?
Her denklemi çözen "tek bir mükemmel yol" malesef yoktur.
Fakat hedefimize ulaştık diyebilmek için denklemi aşağıdaki şekilde yazabilmeliyiz:
x = bir şeyler
Diğer bir deyişle, bilinmeyeni (Bu örnekte "x") bir tarafta yalnız bırakabilmeliyiz.
Örneğin: 3x−6 = 9 denkleminin çözüm kümesi nedir?
| Bununla başlayın | 3x−6 = 9 | |
| Her iki tarafa 6 ekleyin: | 3x = 9+6 | |
| 3'e bölün: | x = (9+6)/3 |
Artık x = bir şey'e sahibiz,
ve basit bir hesaplamayla x = 5 olduğu ortaya çıkıyor
Yapboz Çözermiş Gibi
Aslında, denklem çözümü yapboz çözmeye benzer. Şunları kullanarak yardım alabiliriz:
Denklem çözerken neler yapabiliriz:
- Kesirleri payda ile çarparak tam sayılara dönüştürebiliriz
- Her iki tarafı da aynı sayılarla toplayıp çıkarabiliriz
- Her iki tarafı sıfırdan farklı bir sayıya bölebiliriz
- Benzer terimleri bir araya getirebiliriz
- Faktöriyel haline getirebiliriz
- Faktöriyeli açabiliriz
- İki kare farkı, İki sayının farkının-toplamının karesi gibi özel kuralları uygulayabiliriz
- Bazen bir fonksiyonu her iki tarafa da uygulayabiliriz
Example: √(x/2) = 3 denklemini çözünüz.
| Başlayın | √(x/2) = 3 | |
| Her iki tarafın kare kökünü alın: | x/2 = 32 | |
| 32 = 9: | x/2 = 9 | |
| Her tarafı 2 ile çarpın: | x = 18 |
Zamanla "kestirme yollar, ipuçları" öğrenerek daha iyi denklem çözebilirsiniz.
Sağlama Yapın
Daima "çözüm" gerçekten bir çözüm mü? diye kendimize sormalıyız.
Nasıl Sağlama Yaparız
Çözümü ya da çözümleri denklemimizde yerlerine koyarız ve çalışıyor mu bakarız.
Örneğin: x'i bulunuz:
2xx − 3 + 3 = 6x − 3 (x≠3)
x≠3 olamayacağını söylememizin nedeni, bir sayıyı sıfıra bölmekten kaçınmamızdır.
Tüm terimleri (x − 3) ile çarpalım:
2x + 3(x−3) = 6
6'yı sola getirelim:
2x + 3(x−3) − 6 = 0
Genişletelim ve çözelim:
2x + 3x − 9 − 6 = 0
5x − 15 = 0
5(x − 3) = 0
x − 3 = 0
Denklem x=3 olursa çözülebiliyor
Şimdi kontrol edelim:
2 × 3 3 − 3 + 3 = 6 3 − 3
İşte Orada Dur!
Bunun anlamı sıfıra bölünmek demek!
Üstelik soruda x≠3 olamaz da denmiş, o halde ...
x = 3 gerçekte işe yaramıyor, ve:
Bu bir çözüm değildir
Bu ilginç ... Bir çözüm bulduğumuzu düşünmüştük fakat kontrol ettiğimizde çözüm olamayacağını gördük!
Bu dersin en önemli tavsiyesi geliyor:
"Denklemi Çözmek" sadece muhtemel çözümleri bize verir, onların kontrol edilmeye ihtiyaçları vardır!