Fonksiyon Nedir?

Bir fonksiyon bir değeri başka bir değere bağlayan bağıntıdır.

Bu girdileri ve çıktıları olan bir makina gibidir.

Ve makinadan çıkanlar bir şekilde girenle bağlantılıdır.

  f(x)  

"f(x) = ... " bir fonksiyon yazmanın en klasik yoludur.
Ve farklı yollar da vardır, daha sonradan göreceğiniz gibi ...

Girdi, Bağıntı, Çıktı

Bir fonksiyon üç temel parçadan oluşur:

  • Girdi
  • Bağıntı
  • Çıktı

Örneğin: "2 ile çarpmak" basit bir fonksiyondur.

Bunun üç parçası vardır:

Girdi Bağıntı Çıktı
0 × 2 0
1 × 2 2
7 × 2 14
10 × 2 20
... ... ...

Eğer girdimiz 50 olsaydı, çıktı kaç olurdu?

Fonksiyonlara Örnekler

  • x2 (karesini almak) bir fonksiyondur
  • x3+1 da bir fonksiyondur
  • Trigonometride kullanılan sinus, kosinüs ve tanjant da birer fonksiyondur
  • daha pek çok örnek verilebilir

Şimdilik özel fonksiyonlara bakmayacağız ...
... onun yerine fonksiyonun temel mantığını kavramamız gerekli.

Fonksiyonun Adı

Öncelikle fonksiyonumuza bir isim vermeliyiz. Bu oldukça yararlı bir şey.

En çok verilen isim "f", fakat "g" de verebilirsiniz ... veya çok istiyorsak "börek" adını da verebiliriz.

Biz şimdilik "f" kullanalım:

f(x)

"x'in f'si x'in karesine eşittir" dedik.

Bir fonksiyonun adını yazdıktan sonra parantez () ve içerisine girdi olarak kabul edeceğimiz değeri ekleriz:

O halde f(x) "f", ve girdiyi belirten "x"

Ve bir fonksiyonu yorumlarken şöyle yapmalıyız:

f(x) = x2 "f" fonksiyonu "x"'i alır ve karesini verir.

 

Örnek: f(x) = x2 ile:

  • Girdi 4 olsun
  • Bu durumda çıktı 16 olacaktır

Şu şekilde yazabiliriz f(4) = 16.

 

"x" Sadece Yer Tutucudur!

Çok fazla "x"'i düşünmenize gerek yok, o sadece girdinin ne olduğunu ve ne şekilde çıktığını bize gösteriyor.

Bu fonksiyon:

f(x) = 1 - x + x2

Şunlarla aynıdır:

  • f(q) = 1 - q + q2
  • h(A) = 1 - A + A2
  • w(θ) = 1 - θ + θ2

(x, q, A, etc) gibi değişkenler sadece değerleri nereye yazacağımızı bilmemiz içindir:

f(2) = 1 - 2 + 22 = 3

 

Bazen Fonksiyonların Adı Yoktur

Bazen isimsiz fonksiyonlar da vardır, biz onları sadece şöyle görürüz:

y = x2

Fakat onların da:

  • bir girdisi (x)
  • bir bağıntısı (karesi)
  • ve bir çıktısı (y) vardır

Bağıntı

Yazının en başında fonksiyonlar makinaya benzer demiştik. Fakat gerçekte onların dişlileri ve hareket eden parçaları yoktur, içine bir şeyler atarak kolaylıkla yok edemezsiniz!

Bir fonksiyon bir girdiyi bir çıktıya bağlar.

"f(4) = 16" demek 4, bir şekilde 16'ya bağlanıyor demektir. Diğer bir deyişle 4 → 16

Örnek: Bu ağaç her yıl 20 cm büyür, o halde ağacın yüksekliği ile yaşı arasında bir bağıntı vardır:

h(yaş) = yaş × 20

Eğer 10 yaşındaysa yüksekliği:

h(10) = 10 × 20 = 200 cm

Başka örnekler verelim:

yaş h(yaş) = age × 20
0 0
1 20
3.2 64
15 300
... ...

 

Fonksiyonlar Neleri İşler?

"Sayılar" oldukça popüler bir cevap, fakat ...

... hangi sayılar?

Yukarıdaki örnekte eğer yaş sıfırdan küçük olsaydı, h(yaş) = yaş×20 bir anlam ifade etmezdi.
... ayrıca harfler de birbirine bağlanabilir ("A"→"B"), veya kimlik numaraları ("39111111111"→"Murat Eliçalışkan") veya daha değişik şeyler de birbirine bağlanabilir.

O halde daha güçlü bir şeyi kullanmaya hazırız, kümeler:

Bir küme bir şeylerin bir arada olmasıdır.

Birkaç örnek:

Çift Tam Sayılar Kümesi: {..., -4, -2, 0, 2, 4, ...}
Kıyafetler Kümesi: {"şapka","tişört",...}
Asal Sayılar Kümesi: {2, 3, 5, 7, 11, 13, 17, ...}
0'dan 10'a kadar 3'ün katları kümesi: {3, 6, 9}

Kümede yer alan her bir şey ("4" veya "şapka" gibi) o kümenin öğesi veya elemanıdır.

O halde fonksiyonlar küme elemanlarını alır ve başka küme elemanları verir.

Bir Fonksiyon Özeldir

Çünkü, fonksiyonların bazı kuralları vardır:

  • Tüm muhtemel girdiler ile çalışabilmesi gerekir
  • Ve her bir girdinin tek bir değeri olmalı

Bu tanımında geçer:

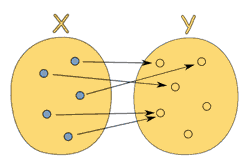Fonksiyonun Tanımı

X ve Y boş olmayan iki küme olmak üzere X'in her elemanını Y'nin yalnız bir elemanına eşleyen f bağıntısına X'den Y'ye bir fonksiyon denir.
(muhtemelen aynı kümede)

İki Önemli Şey

1.

"...her eleman..." X kümesindeki her elemanın Y kümesindeki bir elemanla bağı olması.

Kısacası fonksiyon X kümesinin tüm elemanlarını kapsamalı.

(Fakat Y kümesindeki her eleman kullanılmak zorunda değil)

2.

"...yalnız birine..." fonksiyonun tek çıktı çıkarmasıdır. Bir fonksiyona gönderdiğiniz aynı değişken 2 veya daha fazla sayıda değerde olamaz.

O nedenle "f(2) = 7 veya 9" yanlıştır!

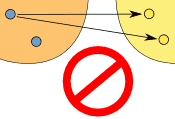
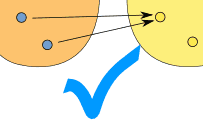
Dikkat: "bir girdi için çok çıktı" kabul edilemez fakat "birden fazla girdi ile tek çıktı" kabul edilebilir:
function   function
(birden ikiye)   (ikiden bire)
Bu bir fonksiyon değildir   Bu bir fonksiyondur

Bir bağıntı yukarıda bahsedilen iki kuralı karşılamıyorsa o halde bu bir fonksiyon değildir ...

Örnek: x → x2 bağıntısı

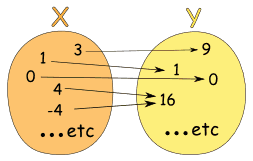
function

Tabloda yazılabilir:

X: x Y: x2
3 9
1 1
0 0
4 16
-4 16
... ...

Bu bir fonksiyondur, çünkü:

  • X'deki her eleman Y'deki en az bir elemanla eşleşmiş
  • X'deki hiçbir eleman Y'de birden fazla elemanla eşleşmemiş

O halde bu kuralları karşılıyor.

(X'deki 4 ve -4'ün Y'deki 16 ile bağlanmış olduğunu fark ettiniz mi? Burada sorun yok!)

Örnek: Aşağıdaki bağıntı bir fonksiyon değildir:

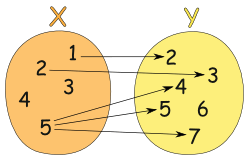
function

Bu bir bağıntı olabilir ama bir fonksiyon değildir, şu sebeplerle:

  • X kümesindeki "3" Y kümesindeki hiçbir elemanla eşleşmemiş
  • Yine X kümesindeki "4" de eşleşmemiş
  • X kümesindeki "5" Y kümesindeki üç elemanla eşleşmiş

(Not: Y kümesindeki "6"'nın eşleşmemiş olması bir sorun yaratmıyor)

 

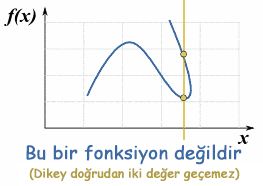not single valued

Dikey Doğru Testi

Tek bir çıktıya sahip olmak demek grafikte dikey bir doğru çizdiğimizde sadece tek bir noktada kesişmesi demektir.

Eğer birden fazla kesişim varsa iyi bir kıvrım olabilir ama fonksiyon değildir.

Sonsuz Değerler

Yukarıda verdiğimiz örneklerde hep az sayıda eleman kullandık. Fakat fonksiyonlar genellikle sonsuz sayıda eleman barındıran kümelerde çalışır.

Örneğin: y = x3

  • Girdimiz "X" kümesi gerçek sayılar kümesi olsun,
  • Çıktımız "Y" kümesi de gerçek sayılar kümesidir

Tüm değerleri gösterebilmemiz imkansızdır:

X: x Y: x3
-2 -8
-0.1 -0.001
0 0
1.1 1.331
3 27
ve daha gidiyor... ve daha gidiyor...

 

Görüntü Kümesi

Yukarıdaki örnekte:

  • Y kümesinde, X kümesindeki elemanlardan en az biriyle eşleşmiş tüm elemanlar fonksiyonun görüntü kümesini oluşturur.

    Basitçe: f(X) = {f(x) : x ∈ X }

Çok Fazla İsim!

Fonksiyonlar Matematikte uzun süredir kullanılıyor ve onları ifade etmek için türlü türlü isimler ve yollar var.

Genelde kullanılan tanımlamalar şöyle:

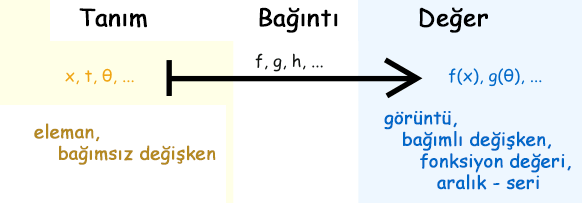
Function Parts

Örnek: z = 2u3:

  • "u", "bağımsız değişken"dir
  • "z", "bağımlı değişken"dir (Çünkü ne olacağı u'ya bağlı)

Bir Fonksiyon Parçalı Olabilir

Girdi değerine göre farklı davranacak fonksiyonlar yazılabilir.

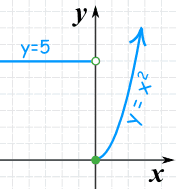
Örneğin: İki parçalı fonksiyon:

  • x 0'dan küçükse, 5 çıktısını verecek
  • x 0 veya daha büyükse, x2 çıktısını verecek
Piecewise Function Çeşitli örnekler:
x y
-3 5
-1 5
0 0
2 4
4 16
... ...

Özet

  • bir fonksiyon girdileri çıktılara bağlar.
  • bir fonksiyon bir küme elemanı ile başka bir kümenin elemanını birbirine bağlar.
  • bir fonksiyonun iki önemli kuralları vardır:
    • Tanım kümesinde her eleman değer kümesindeki herhangi bir elemanla eşleşmeli,
    • Tanım kümesindeki hiçbir eleman değer kümesindeki birden fazla elemanla eşleşmemelidir.

 

Soru 1  Soru 2  Soru 3  Soru 4  Soru 5  Soru 6  
matematik.sitesi.web.tr © 2021
Hazırlayan: Murat ELİÇALIŞKAN