Kümeler Konusuna Giriş
Sayılarla ilgili tüm bildiklerinizi unutun.
Aslında sayı nedir unutun.
Burası Matematiğin başladığı yer.
Sayılarla matematik yerine, "birşeylerle" matematik başlıyor.
Tanım
Küme nedir? Basitçe küme demek bir kolleksiyon demektir.
Öncelikle "ortak özellikleri olan birşeyleri" sınıflayalım.

Örneğin giyindiğiniz eşyalar: ayakkabı, çorap, şapka, tişört, pantolon ve bunun gibiler.
En az 100 eşya sayabilirsiniz.
Bu bir küme oluşturur.
Diğer bir örnek parmaklarınız. Fotoğrafta gösterilen küme işaret parmağı, orta parmak, yüzük parmağı ve serçe parmağınızı içeriyor. |
 |
Bunlar ortak bir özelliğe sahip birlikte gruplanmış "şeyler".
Notlar
Küme elemanlarını (ya da "üyelerini") listelerken virgül ile onları ayırırız ve kıvrımlı parantez içine alırız:

Kıvrımlı parantez { } bazen "küme parantezi" olarak da adlandırılır.
Bu makalenin başında verdiğimiz örneklerle ilgili kullanıma bakalım:
{çoraplar, ayakkabılar, saatler, tişörtler, ...}
{işaret parmağı, orta parmak, yüzük parmağı, serçe parmak}
Fark ettiyseniz ilk örnekte üç nokta ("...") kullanmışız.
Üç nokta ... bir kısaltmadır ve "devam ediyor" anlamı taşır.
İlk örnekte yer alan üç nokta (...) sonsuzluğu ifade eder.
O halde:
- İlk küme {çorap, ayakkabı, saat, tişört, ...} bir sonsuz kümedir,
- İkinci küme {işaret parmağı, orta parmak, yüzük parmağı, serçe parmak} ise sonlu bir kümedir.
Fakat bazen "..." uzun bir listenin orta kısmını ifade edebilir:
Örneğin: Harfler kümesi:
{a, b, c, ..., x, y, z}
Bu durumda bu küme sonlu bir kümedir (29 harf var, değil mi?)
Sayı Kümeleri
Bir küme belirttiysek ortak özelliklere sahip olmalı dedik. Peki sayılar için kümeler oluşturabilir miyiz?
Tek Sayılar Kümesi: {..., -3, -1, 1, 3, ...}
Asal Sayılar Kümesi: {2, 3, 5, 7, 11, 13, 17, ...}
0'dan Büyük 10'dan Küçük 3'ün Katları Kümesi: {3, 6, 9}
Daha pekçok listeleme yapabiliriz.
Ortak bir özelliğe sahip olmasa da sayı kümeleri oluşturabiliriz, bunlar tanımlı kümelerdir. Örneğin:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203}
Yukarıdaki iki örnekteki tüm sayılar rastgele oluşturulmuştur.
Kümeler Neden Önemlidir?
Kümeler, Matematiğin temel bileşenlerindendir. Belki sözler yetersiz gelebilir. Ancak farklı durumlarda kümelerin kullanılması sonucunda çok güçlü ve karmaşık bir Matematik doğmuştur.
Universal Set
 |
Makalenin başında "bir şeyler" demiştik. Bahsettiğimiz şey evrensel kümedir. Bu her şeyi kapsayan bir kümedir. Aslında, tam olarak her şeyi kapsamaz. Sorumuzla alakalı olan her şey desek daha doğru olur. | |
 |
Örneğin kümemiz tam sayıları içersin. Evrensel küme tüm tam sayılar olur. |
Diğer Notlar
 |
Kümeleri ifade ederken küme adları büyük harf ile temsil edilir. Elemanlar ise küçük harfle yazılır. Örneğin, A bir küme ve a bir elemandır. Aynı şekilde B bir küme b bir elemandır. C ve c gibi... |
A kümesindeki a elemanından bahsederken ![]() sembolünü kullanırız.
sembolünü kullanırız.
Eğer o kümenin bir elemanı değilse ![]() işareti kullanılabilir.
işareti kullanılabilir.
Örneğin: A Kümesi {1,2,3} olsun. Görebiliyoruz ki 1 ![]() A, fakat 5
A, fakat 5 ![]() A
A
Eşitlik
Aynı elemanlara sahip kümeler eşit kümelerdir. İlk bakışta eşit görünmeyen kümeler de eşit olabilir, iyi çözümlememiz gerekir.
Örneğin: A ve B kümeleri eşit midir?:
- A ilk dört pozitif tam sayıdan oluşan kümedir
- B = {4, 2, 1, 3}
Kontrol edelim. Her iki küme de 1, 2, 3 ve 4'ü içerir. Her elemanı kontrol ettikten sonra rahatlıkla söyleyebiliriz: Evet, bunlar eşit!
Ve eşitlik işareti (=) kümelerin eşitliğini belirtirken kullanılabilir:
A = B
Alt Küme
Bir küme oluşturduğumuz zaman, o kümedeki elemanlarla yeni kümeler oluşturabiliriz. Bunların her birine alt küme denir.
Örneğin, Elemanları {1, 2, 3, 4, 5} olan bir kümemiz olsun. Bu durumda {1, 2, 3} kümesi bir alt kümedir. {3, 4} de bir alt kümedir, hatta {1} de bir alt kümedir. Ancak {1, 6} bir alt küme değildir. Çünkü kümemizde 6 diye bir eleman yoktur. Genellikle:
A kümesi B kümesinin alt kümesidir, eğer A'daki elemanlar B'de de varsa!
Bu tanımı örneklerle zenginleştirelim.
A = {1, 3, 4} ve B = {1, 4, 3, 2} ise A, B'nin alt kümesi midir?
1 A'da bulunuyor ve B'de de var. İyi görünüyor.
3 A'da var, B'de de var!
A'da 4 var. B kümesinde de var.
A'nın tüm elemanları B'de de bulunuyor. Artık tamam!
Evet, A, B'nin alt kümesidir
Dikkat, 2 B'de var ama A'da yok. Bunun bir önemi yok. Bizim için önemli olan A'da ne olduğudur.
Biraz daha zorlaştıralım.
Örnek: A kümesi 4'ün katlarından ve B kümesi 2'nin katlarından oluşuyor. Bu durumda A, B'nin alt kümesi midir? B, A'nın alt kümesi midir?
Bu durumda tek tek tüm elemanları kontrol edemeyiz, çünkü bu kümeler sonsuz sayıda elemana sahipler. O halde bir fikre ihtiyacımız var. Nasıl görünüyorlar bir bakalım:
Kümeler:
- A = {..., -8, -4, 0, 4, 8, ...}
- B = {..., -8, -6, -4, -2, 0, 2, 4, 6, 8, ...}
Bir şeyi fark ediyoruz A'da bulunan her eleman B'de de var. Fakat B'de olan bazı elemanlar A'da bulunmuyor:
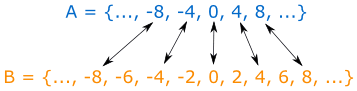
O halde:
A, B'nin alt kümesidir, fakat B, A'nın alt kümesi değildir
Bir kümenin alt küme sayısını 2n formülü ile buluruz. Burada belirtilen n, eleman sayısıdır.
Örneğin 2 elemanı olan bir kümenin 22 = 4 alt kümesi vardır. 5 elemanı olan bir küme ise 25 = 32 alt kümeye sahiptir.
Öz Alt Küme
Alt kümelerden biri kümedeki tüm elemanları barındırıyorsa ne olur?
Düşünelim: A bir küme olsun. Bu kümedeki her elemanın bulunduğu bir küme A'nın alt kümesi olabilir mi?
Bu pek mantıklı gelmiyor, değil mi? Alt kümelerin birbirinden farklı olması beklenir. İşte kümenin kendisinden farklı olan tüm alt kümeleri öz alt küme olarak adlandırılır.
Kısaca bir kümenin kendisi, o kümenin tam olarak bir alt kümesi değildir.
Örnek:
{1, 2, 3} kümesi {1, 2, 3} kümesinin alt kümesidir, fakat öz alt kümesi değildir
Örnek:
{1, 2, 3} kümesi {1, 2, 3, 4} kümesinin alt kümesidir ve aynı zamanda öz alt kümesidir. Çünkü 4 elemanı ilk kümemizde bulunmuyor.
Dikkat: Her öz alt küme, aynı zamanda alt kümedir.
Bir kümenin öz alt küme sayısını 2n − 1 formülü ile buluruz.
Örneğin 3 elemanlı bir kümenin 23 − 1 = 7 öz alt kümesi vardır.
Bir Kümenin Diğerini Kapsaması
A, B'nin alt kümesi ise, A ![]() B, eğer alt kümesi değilse, A
B, eğer alt kümesi değilse, A ![]() B şeklinde yazarız.
B şeklinde yazarız.
Boş Küme
Kümelerle ilgili en tuhaf şeyi dinlemeye hazır olun.

Örneğin, piyano tuşları bulunan gitarlar kümesini düşünelim.
Fakat bir dakika! "Bir gitarda piyano tuşu bulunmaz ki!"
Bu kümenin hiçbir elemanı yoktur.
Bu tarz kümelere boş küme denir. İçinde hiçbir eleman yoktur. Sıfır elemanlıdır.
Elemansız bir küme ![]() ya da {} ile gösterilir.
ya da {} ile gösterilir.
Boş kümeye diğer bir örnek Güney Kutbunun güneyindeki ülkeler dir.
Peki boş kümeye neden tuhaf dedik, sıradaki bölümde açıklıyoruz...
Boş Küme ve Alt Kümeler
Alt kümenin tanımını hatırlayalım: Bir küme oluşturduğumuz zaman, o kümedeki elemanlarla oluşturulan kümelerdir. O halde hiçbir elemanı olmayan boş küme A'nın alt kümesi olabilir mi?
Tabiki olabilir. Hiçbir elemanı kullanmamayı seçebiliriz. Bu durumda A kümesi içerisinde bir boş küme elde ederiz.
Boş küme, her kümenin alt kümesidir, kendisi de dahil.
Eleman Sayısı
Bir kümenin eleman sayısı s(A) ya da n(A) şeklinde gösterilir.
Örneğin: A = {1,2,3,4}, B = {5,6,7} ise s(A) = 4, s(B) = 3 tür.