Mutlak Değerin Cebirde Kullanımı
Bir sayının mutlak değeri, onun sıfıra olan uzaklığıdır. Sayı pozitif ya da sıfırsa olduğu gibi bırakırız, negatifse pozitif ile değiştiririz.
x aşağıdaki değerlere eşit olabilir:
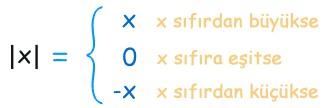
Mutlak değerden çıkan sonuçlar aşağıdaki gibi olur:
- x sıfırdan büyükse, x
- x sıfır ise, 0
- x sıfırdan küçükse, −x (bu durumda sayıyı "pozitif" yaparız)
Örnek: |−17| kaçtır?
Sayı sıfırdan küçük olduğundan "−x" hesaplanır:
− ( −17 ) = 17
(Çünkü eksinin eksiyle çarpımı artıdır)
Çeşitli Özellikler
İşlemlerinizde faydalı olabilecek bazı özellikler:
|a| ≥ 0 daima!
Unutmayın |a| asla sıfırdan küçük olamaz.
|a| = √(a2)
a'nın karesi pozitif ya da sıfırdır (eğer a gerçek sayıysa). Sonuç olarak kare durumundaki sayının kökü pozitif ya da sıfırdır.
|a × b| = |a| × |b|
Bunlar aynı anlama gelir:
- (a çarpı b)'nin mutlak değeri, ve
- (a'nın mutlak değeri) çarpı (b'nin mutlak değeri).
Sıradaki özellik soruları çözerken size çok faydalı olacak:
|u| = a eşittir u = ±a ve bunun tersine
Bu özellik birçok mutlak değer sorusu çözümüne yardım eder.
Örnek: |x+2|=5 çözünüz.
"|u| = a ile u = ±a aynıdır":
| bu: | |x+2|=5 | |
| bununla aynıdır: | x+2 = ±5 |
Bu durumda çözüm kümesinin iki elemanı olur:
| x+2 = −5 | x+2 = +5 |
| x = −7 | x = 3 |
Grafikte Gösterelim
Belirtilen örneğin çözüm kümesini grafikte gösterelim:
|x+2| = 5
Eğer denklem sıfıra eşitse grafik çizmek daha kolay olur ("=0"). Bunun için denklemin her iki tarafından 5 çıkarırız.:
|x+2| − 5 = 0
Grafiğimizi çizmeye başlarız:
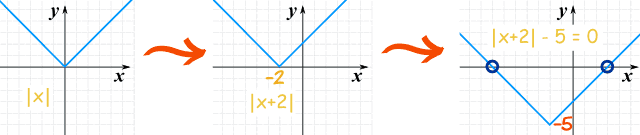 |
||
| |x| | |x+2| | |x+2|-5 |
Buna göre iki çözüm olduğu görülebiliyor: −7 veya +3.
Mutlak Değerli Eşitsizlikler
Mutlak değer ve eşitsizlikler konusunu birleştirdiğimiz zaman biraz daha dikkatli olmamız gerekir!
4 eşitsizlik vardır:
| < | ≤ | > | ≥ | |
|---|---|---|---|---|
| küçüktür | küçük veya eşittir |
büyüktür | büyüktür veya eşittir |
Küçüktür, Küçük-Eşittir
Eğer "<" ve "≤" kullanılmışsa sıfırı ortalayan tek bir aralık vardır:
Örnek: |x| < 3
Bu x'in sıfıra uzaklığı 3'ten küçük demektir:
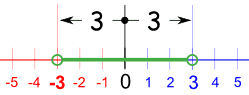
-3 ile 3 arasındaki her sayı olabilir (ama bu sayılar olamaz)
Aşağıdaki şekilde yazılabilir:
−3 < x < 3
Aralık şu şekilde gösterilebilir: (−3, 3)
"Küçük veya Eşittir" için de aynı şey yapılır:
Example: |x| ≤ 3
-3 ile 3 arasındaki her şey ve -3 ile 3 dahil.
Aşağıdaki şekilde yazılabilir:
−3 ≤ x ≤ 3
Aralık şu şekilde gösterilebilir: [−3, 3]
Daha büyük bir örneğe ne dersiniz?
Örnek: |3x-6| ≤ 12
Aşağıdaki şekilde tekrar yazalım:
−12 ≤ 3x−6 ≤ 12
6 ekleyelim:
−6 ≤ 3x ≤ 18
Son olarak (1/3) ile çarpalım. Çünkü pozitif bir sayıyı çarpmak eşitsizlikte bir değişikliğe yol açmaz.:
−2 ≤ x ≤ 6
İşte bitti!
Aralık aşağıdaki şekilde yazılabilir: [−2, 6]
Büyüktür ve Büyük-Eşittir
Bu biraz farklı ... iki farklı aralık elde edilir:
Example: |x| > 3
Bu grafikte aşağıdaki gibi görünür:
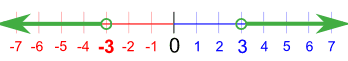
-3'den küçük ya da 3'ten büyük
Aşağıdaki şekilde yazılabilir:
x < −3 veya x > 3
Aralık: (−∞, −3) U (3, +∞)
Dikkat! Aşağıdaki şekilde yazmayın
−3 > x > 3 ![]()
"x" aynı anda -3'ten küçük ve 3'ten büyük olamaz.
Aslında şöyledir:
x < −3 veya x > 3 ![]()
"x" −3'ten küçük veya 3'ten büyüktür
Aynı durum "Büyük veya eşittir" için geçerlidir:
Örnek: |x| ≥ 3
Aşağıdaki şekilde yazılabilir
x ≤ −3 veya x ≥ 3
Aralığı göstermek istersek: (−∞, −3] U [3, +∞)