Polinomlar
Bir polinom aşağıdaki gibi görünür:
 |
| 3 terimli bir polinom örneği |
Polinom poly- ("çok") ve -nomial ("terim") ... kelimelerinden türetilmiştir. Kısaca "çok terimli" anlamına gelir
Bir polinom üç şeye sahip olabilir:
| kat sayı (3, -20, veya ½ gibi) |
| değişkenler (x ve y gibi) |
| üsler (y2 ifadesindeki 2 gibi), sadece 0, 1, 2, 3, ... olabilir! |
Polinomlarla toplama, çıkarma, çarpma, bölme işlemleri yapılabilir
... fakat ...
| ... bir değişkene bölünemezler (yani şöyle bir şey olamaz: 2/x) |
So:
Bir polinom kat sayılar, değişkenler ve üsler içerebilir,
buna karşın asla bir değişkene bölünemezler.
Polinom Mu Değil Mi?
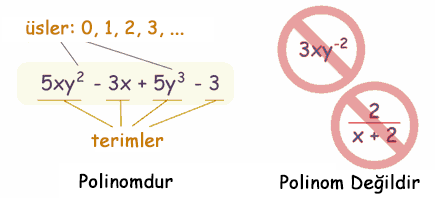
Şunlar birer polinomdur:
- 3x
- x - 2
- -6y2 - (7/9)x
- 3xyz + 3xy2z - 0.1xz - 200y + 0.5
- 512v5+ 99w5
- 5
(Evet, sadece "5" de bir polinomdur, tek terimi vardır ve sabit bir değere sahiptir)
Aşağıdakiler ise polinom değildir:
- 3xy-2 değil, çünkü üs "-2" (üsler sıfır ve pozitif tam sayılar olabilir)
- 2/(x+2) değil, çünkü bir değişkene bölünemezler
- 1/x yine değil
- √x değil, çünkü üs "½" olamaz
Fakat şunlar polinomdur:
- x/2 polinomdur, çünkü sabit bir sayıya bölünebilirler
- ayrıca 3x/8 yine aynı sebeple olabilir
- √2 de olabilir, çünkü bu sabit bir değerdir (= 1.4142...vb)
Monom, Binom, Trinom
Türkçede fazla aşina olmasanız da değinelim. Bunlar 1, 2 ve 3 terimli polinomların özel isimleridir:
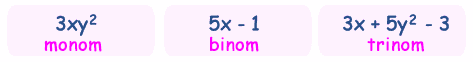
| İsimlerini unutmamak için bisiklet örneği verelim! |
 |
Polinomlar Çok Fazla Terime Sahip Olabilir Mi?
Birçok terime sahip olabilirler ancak sonsuz sayıda olamazlar
Değişkenler
Polinomlar hiçbir değişkene sahip olmayabilir
Örneğin: 21 bir polinomdur. Sabit bir değere sahip tek terimlidir.
Veya bir değişkene sahip olabilirler
Örneğin: x4-2x2+x üç terimlidi ve tek bir değişkene sahiptir (x)
İki ve daha fazla değişkene de sahip olabilir
Örneğin: xy4-5x2z iki terime ve üç değişkene (x, y ve z) sahiptir
Polinomları Özel Kılan Nedir?
Polinomlar kesin tanımlıdır ve kolaylıkla işlemlerde kullanılabilir.
Örneğin:
- Polinomların toplanması ve çıkarılması yine bir polinom verir.
- Polinomları çarparak da yine polinom elde edilebilir.
Ayrıca, polinomlar kolaylıkla grafikte gösterilebilir.
Örneğin: x4-2x2+x
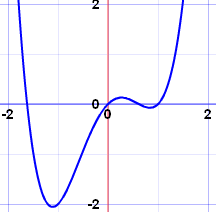 |
Güzel bir grafik |
Ayrıca polinomları bölebilirsiniz (ancak sonuç polinom çıkmaz).
Derece
Bir polinomun derecesi aynı terimdeki değişkenlerin üslerinin toplamının en büyük olanıdır..
Örneğin:
| Derece 3'tür (x'in en büyük üssü) |
NOT: Değişkenler farklı da olsa derece hesabında bir terimdeki üsler toplanır. Örneğin; xy2 polinomunun derecesi 3, 5y2z2 polinomunun derecesi 4 deriz.
Bir Polinomun Standart Biçimi
Bir polinomun standart yazılışında derecesi en büyük olan en başa yazılır. Büyükten küçüğe doğru terimler sıralanır.
Örneğin: Şunu standart formda yazalım: 3x2 - 7 + 4x3 + x6
En yüksek derece 6, o halde onu en başa yazarız, sonra 3, 2 ve en son sabit terim yazılır:
x6 + 4x3 + 3x2 - 7
Standart biçimi kullanmak zorunlu değildir ancak işlemlerde işinizi kolaylaştırabilir.