Polinomlarda Çarpma İşlemi

Bir polinom aşağıdaki gibi görünür:

İki polinomu birbiriyle çarparken:

• Polinomun Her terimi, çarpılan polinomun her terimi ile çarpılır.
• Sonra, tüm sonuçlar toplanır ve varsa sadeleştirmeler yapılır

Basit örneklerden yola çıkarak polinomları çarpmayı öğrenelim.

1 terimli polinom × 1 terimli polinom

Terimleri birbiri ile çarparken, öncelikle kat sayıları birbiriyle çarparız, ondan sonra her değişkeni birbiriyle çarparız, şunun gibi:

(Not: Çarpım işlemini gösterirken çarpma işareti yerine "·" kullandık. Matematiksel işlemlerde bazen "×" kullanılmaz. Çünkü bu işaret değişken olarak belirtilen "x"'e çok benzer.)

Üslü sayılar çarpılırken üslerin toplandığını hatırlayınız.

1 terimli polinom × 2 terimli polinom

Tek terimli polinomu, iki terimlinin her terimiyle çarparız, şunun gibi:

2 terimli polinom × 1 terimli polinom

Yine aynı şekilde tek terimliyi, iki terimlinin iki terimi ile ayrı ayrı çarparız:

2 terimli polinom × 2 terimli polinom

İlk polinomdaki iki terim ...

... ikinci polinomdaki iki terimle

... ayrı ayrı çarpılır

Bu durumda 4 çarpım yapmamız gerekir ... Neden?

İki terimli polinomları (binomları) çarparken de bu kural geçerli.

Murat ve Fatoş yerine a ve b, Oğuz ve Ece yerine c ve d dersek:

Genellikle bu çarpıma içler dışlar çarpımı diyorlar.

İlkler: ac Dışlar: ad İçler: bc Sonlar: bd

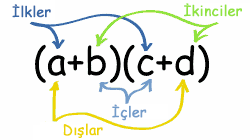Bunu bir örnekte görelim;

2 terimli polinom × 3 terimli polinom

Bu makalenin başında ne yazmıştık?:

Polinomları çarparken, ilk polinomun her bir terimini
diğer polinomun her bir terimi ile çarparız.

Benzer Terimler

Ve daima benzer terimlerin toplanması gerektiğini hatırlayın: