Kümeler ve Venn Şeması

Kümeler

Küme, birbirindan farklı, iyi tanımlanmış nesneler topluluğudur.

Bir örnek verecek olursak, üzerinizdeki kıyafetler bir küme oluşturur: ayakkabı, çorap, şapka, tişört, pantolon bu kümenin elemanlarıdır.

Kümeyi belirtirken kıvrımlı parantez kullanılır, tıpkı şunun gibi:

{çorap, ayakkabı, saat, tişört, pantolon, ...}

Sayıların da kümeleri vardır:

• Doğal Sayılar Kümesi: {0, 1, 2, 3, ...}
• Asal Sayılar Kümesi: {2, 3, 5, 7, 11, 13, 17, ...}

On İyi Arkadaş

En iyi on arkadaşınızı bir kümede gösterelim:

• {ayşe, ali, yusuf, emre, selen, oğuz, murat, rabia, fatoş, ece}

Her arkadaşınız kümenin bir "elemanıdır" (ya da "üyesidir"). Küme elemanları için küçük harfler kullanılır.

 

Arkadaşlarınızdan ayşe, yusuf, murat ve fatoş futbol oynuyorlar:

Futbol = {ayşe, yusuf, murat, fatoş}

("Futbol" kümesi ayşe, yusuf, murat ve fatoş elemanlarından oluşur)

ve ali, murat, fatoş Tenis oynuyorlar:

Tenis = {ali, murat, fatoş}

Birbirinden farklı iki çember içinde bu isimleri yazalım:

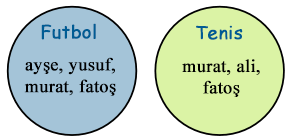
Birleşim

Şimdi arkadaşlarınızdan Futbol VEYA Tenis oynayanları listeleyelim.

Buna "Birleşim" diyeceğiz ve ∪ işareti ile göstereceğiz:

Futbol ∪ Tenis = {ayşe, ali, yusuf, murat, fatoş}

Tüm arkadaşlarınız bu kümede değil ... sadece Futbol veya Tenis (ya da her ikisini de) oynayan arkadaşlarınız listelendi.

Birleşim kümesini "Venn Şeması"nda gösterelim:

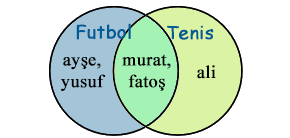
Venn Şeması: İki Kümenin Birleşimi

Venn Şeması kullanmak akıllıca, çünkü bu size birçok bilgi verebilir:

Kesişim

"Kesişim" iki ya da daha fazla kümenin ortak elemanlarını gösterir.

Örneğimize göre hem futbol hem tenis oynayanlar kesişim kümesini oluşturur ... murat ve fatoş'un olduğu küme.

Kesişimi göstermek için ters "U" işaretini kullanırız: ∩

Ve kesişim kümemiz şu şekilde yazılabilir:

Futbol ∩ Tenis = {murat, fatoş}

Venn şemasında:

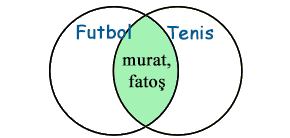
Venn Şeması: İki Kümenin Kesişimi

 

Fark

Kümeleri birbirinden "çıkarabilirsiniz".

Örneğin, Futbol kümesinden Tenis kümesini çıkarırsak sadece futbol oynayanların oluşturduğu küme elde edilir ... ayşe ve yusuf'tan oluşan küme.

Ve aşağıdaki şekilde yazılabilir:

Futbol − Tenis = {ayşe, yusuf}

Venn Şemasında:

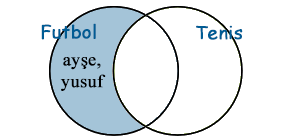
Venn Şeması: İki Kümenin Farkı

Özetle

∪ birleşimdir: kümelerden herhangi birinde olan
∩ kesişimdir: her iki kümede de bulunan
− farktır: birinde olup diğerinde olmayan

Üç Küme

Venn şemasında üç küme de gösterebilirsiniz.

Yukarıdaki örnek ile devam edelim. Yeni bir küme ekliyoruz. Adı "Voleybol", oyuncuları murat, ali ve ece olsun:

Voleybol = {murat, ali, ece}

Fakat biraz daha "matematiksel" olalım ve kümelerin adını büyük harfle belirtelim:

• F futbol oynayanlar kümesi,
• T tenis oynayanlar kümesi,
• V voleybol oynayanlar kümesi anlamına gelsin

Venn şeması aşağıdaki şekilde görünecektir:

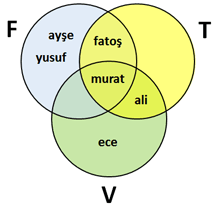
Üç Kümenin Birleşimi: F ∪ T ∪ V

Şemaya baktığınızda şunları görebiliyor musun:

• murat Futbol, Tenis ve Voleybol oynuyor
• ali Tenis ve Voleybol oynuyor
• ayşe ve yusuf Futbol oynuyor, fakat Tenis ya da Voleybol oynamıyor
• sadece Tenis oynayan biri yok

Kesişim ve birleşim ile konuya biraz daha eğlence katalım:

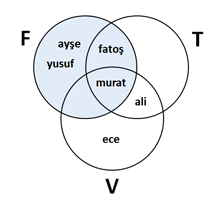
Bu F Kümesi

F = {ayşe, yusuf, fatoş, murat}

 

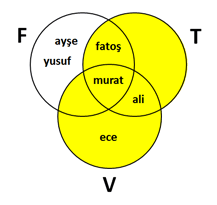
Bu T ve V kümelerinin birleşimi

T ∪ V = {fatoş, murat, ali, ece}

 

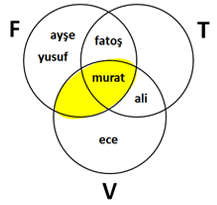
Bu F ve V kümelerinin kesişimi

F ∩ V = {murat}

Şimdi size bir sorumuz var ...

• az önce gösterilen F ∩ V kümesinden
• T kümesi çıkarılırsa ne olur?

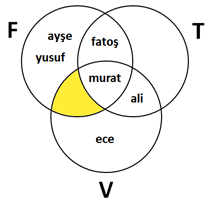
Bu F ve V kümelerinin kesişiminden T kümesini çıkarmaktır

(F ∩ V) − T = {}

Hey, burada bir şey yok!

Bu bir "Boş Küme" dir. Belirtirken içi boş kıvrımlı parantez kullanılır: {}

Boş Küme hiçbir elemanı olmayan kümedir: {}

Evrensel Küme

Evrensel Küme her şeyin kümesidir. Aslına bakarsanız tam olarak her şey değildir. İlgilendiğimiz her şey desek daha doğrudur.

Yukarıda bahsedilen durumda evrensel kümemiz 10 iyi arkadaşımızdır.

E = {ayşe, ali, yusuf, emre, selen, oğuz, murat, rabia, fatoş, ece}

Evrensel kümeyi venn şemasında gösterebiliriz. Bunun için tüm elemanları kapsayan bir çerçeve çizeriz:

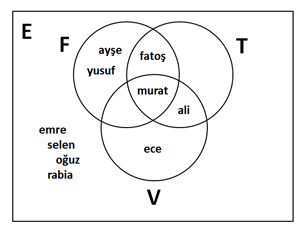
Artık tüm iyi arkadaşlarınızı görebiliyorsunuz, temiz bir şekilde, oynadıkları spor dallarına göre ...

Varsayalım, futbol oynamayanları görmek istiyoruz. Yapmamız gereken tüm arkadaşlarımızdan futbol oynayanları çıkarmak:

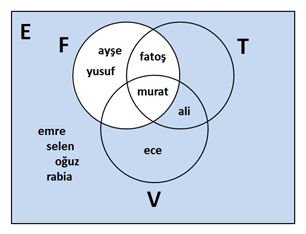
Şu şekilde yazabiliriz:

E − F = {ali, ece, emre, oğuz, selen, rabia}

"Evrensel kümeden futbol oynayanların kümesinin çıkarılmasıyla oluşan küme: {ali, ece, emre, oğuz, selen, rabia}"

Diğer bir deyişle "futbol oynamayan herkes".

Bir Kümenin Tersi

"Belirtilen küme dışındaki her şey" anlamına gelir.

Bir kümenin tersini gösterirken üst ayraç "'" kullanılır, şunun gibi:

F^'

Yukarıdaki ifadeden şu anlam çıkar "F kümesi hariç her şey", belirttiği alanı işaretlersek:

F^' = {ali, ece, emre, oğuz, selen, rabia}
(Tıpkı üstte yer alan E − F örneğindeki gibi)

 

Özet

A^' bir kümenin tersidir: A'da olmayan her şey
Boş Küme: Elemanı olmayan kümedir. {} ya da Ø ile gösterilir
Evrensel Küme: alakalı olan her şeydir